

- #Differential system of equations solver update#
- #Differential system of equations solver code#
- #Differential system of equations solver windows#
Second, the simulation time parameters are included in a vector, indicating that the equations should be solved starting at time zero and ending at t_end. First, the file containing the system equations (suspension_model.m described below) is included after the symbol, indicating a function handle. The ode45 command uses three parameters to describe how the simulation should run. Several other ODE solvers are available (e.g., ode23 and ode113) that may be more appropriate for certain equations. The command ode45 is MATLAB’s differential equation solver that can be used for nonstiff 1 ordinary differential equation problems with a medium order of accuracy. The next line is the one that solves the system equations given by (2.3). These values are used to solve the system equations. In this simulation, the wheel height, car height, and their derivatives set to zero, meaning the system is initially at rest. In these four lines, the initial conditions are set for the system. We may wish to associate any system of units with (2.3), but in this example and throughout the book, we generally use SI units. Rather, it is up to the user to interpret the results and associate appropriate units with the values.
#Differential system of equations solver code#
This value is used later in the code to solve the system equations for the specified amount of time (5 seconds in this case). Next the simulation time is set and stored in the t_end variable.
#Differential system of equations solver windows#
These first two lines of the code close figure windows and clear variables so that the simulation is starting with a clean slate. We now discuss the above code in detail and describe each line. Legend('Wheel Height, x_1','Car Height, x_2') % Close all figures and clear all variables

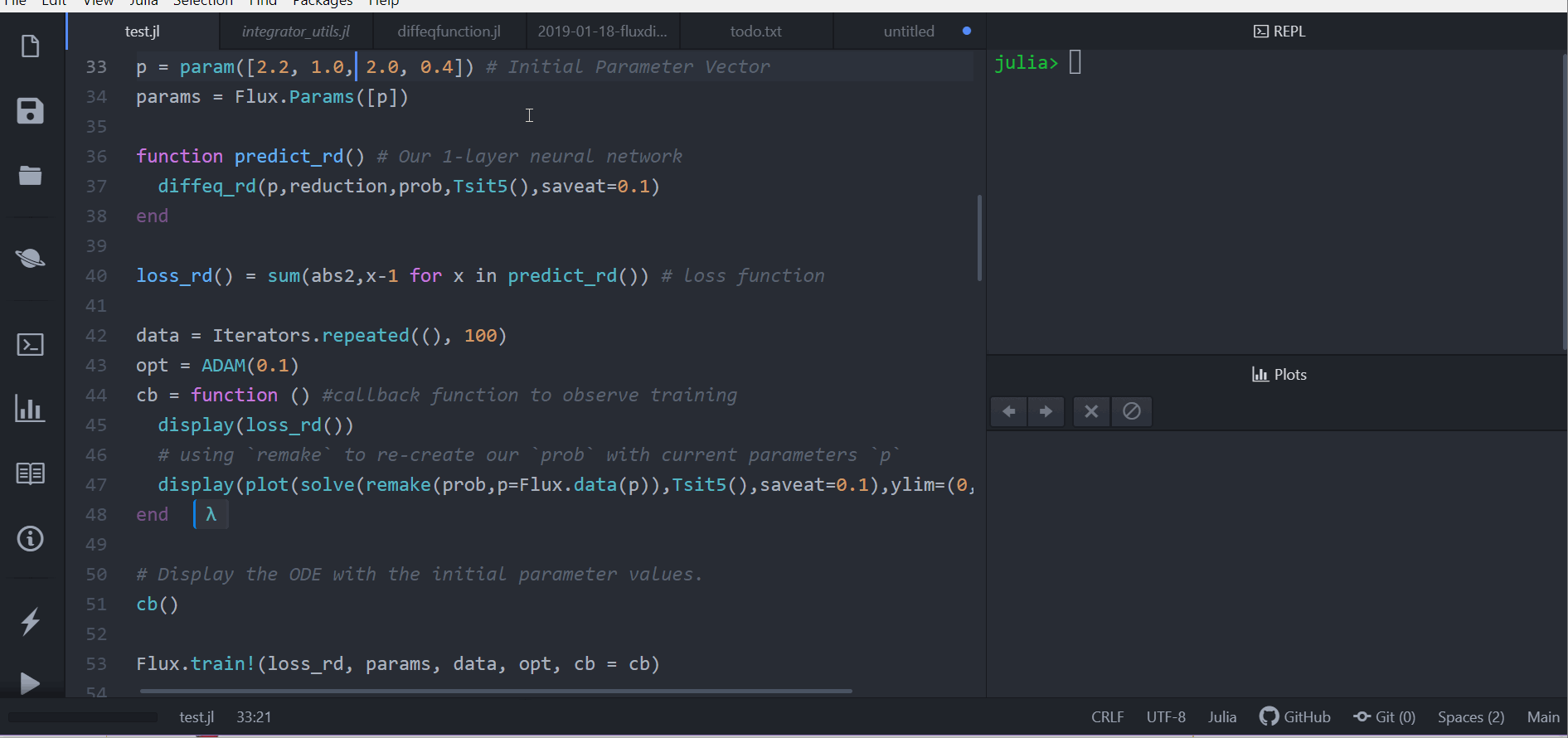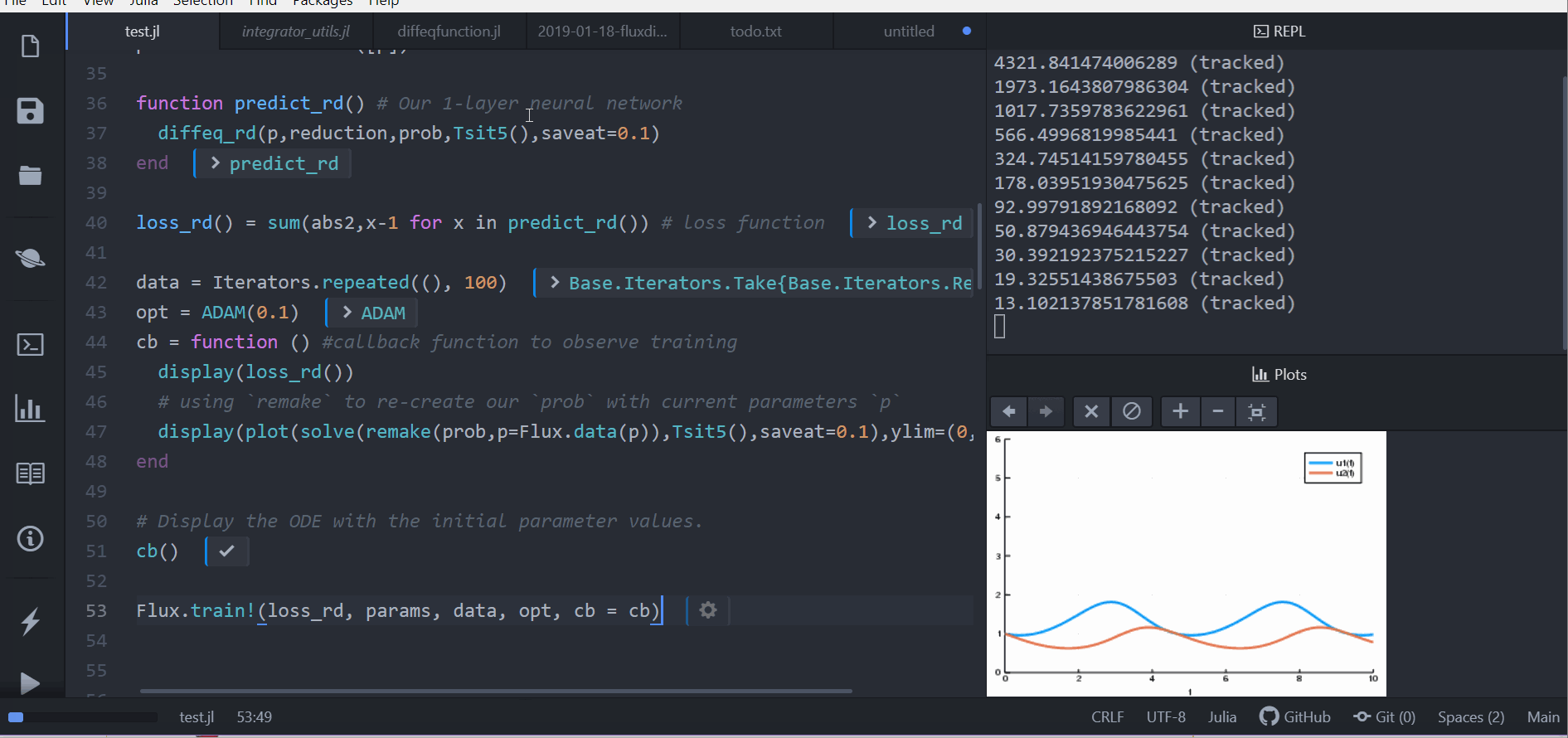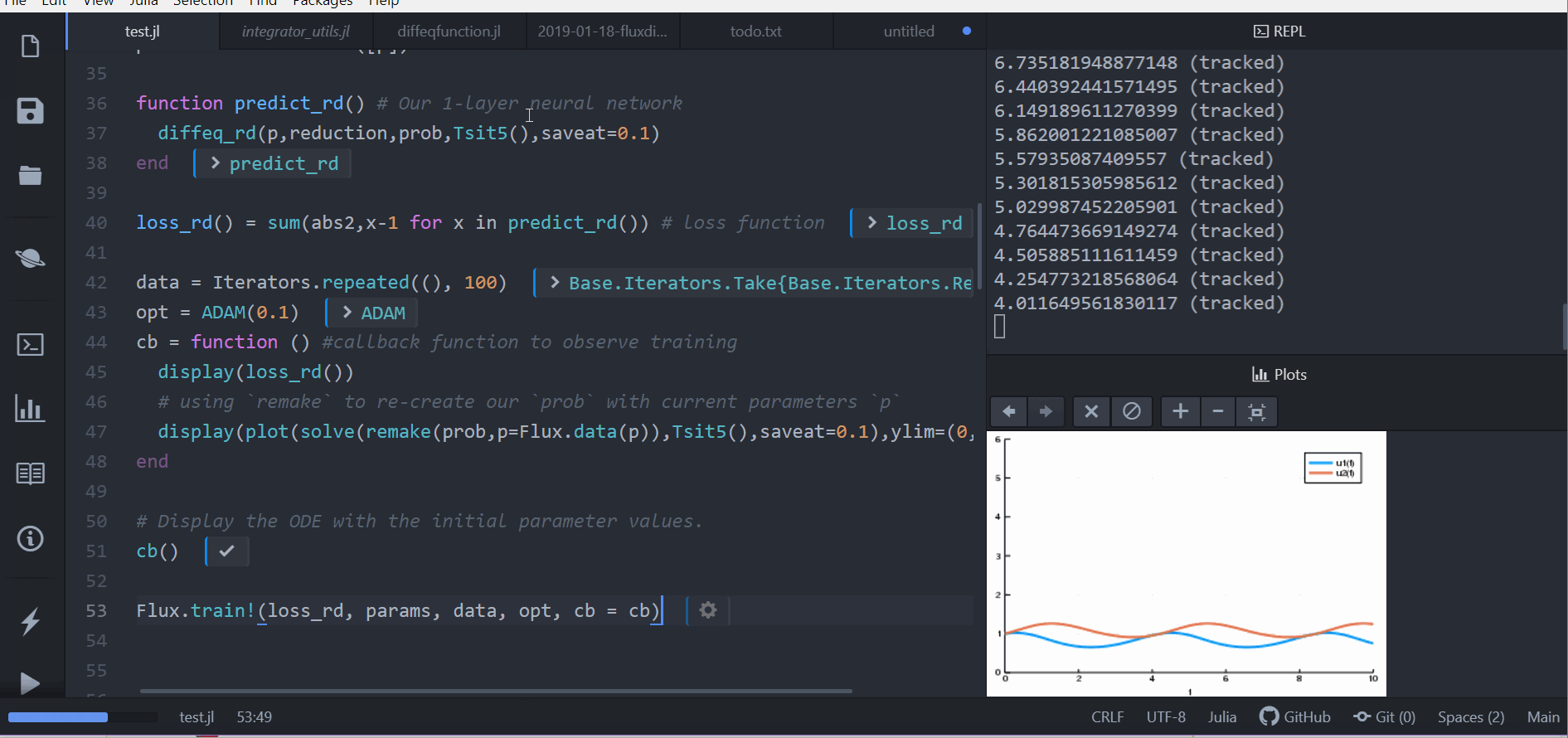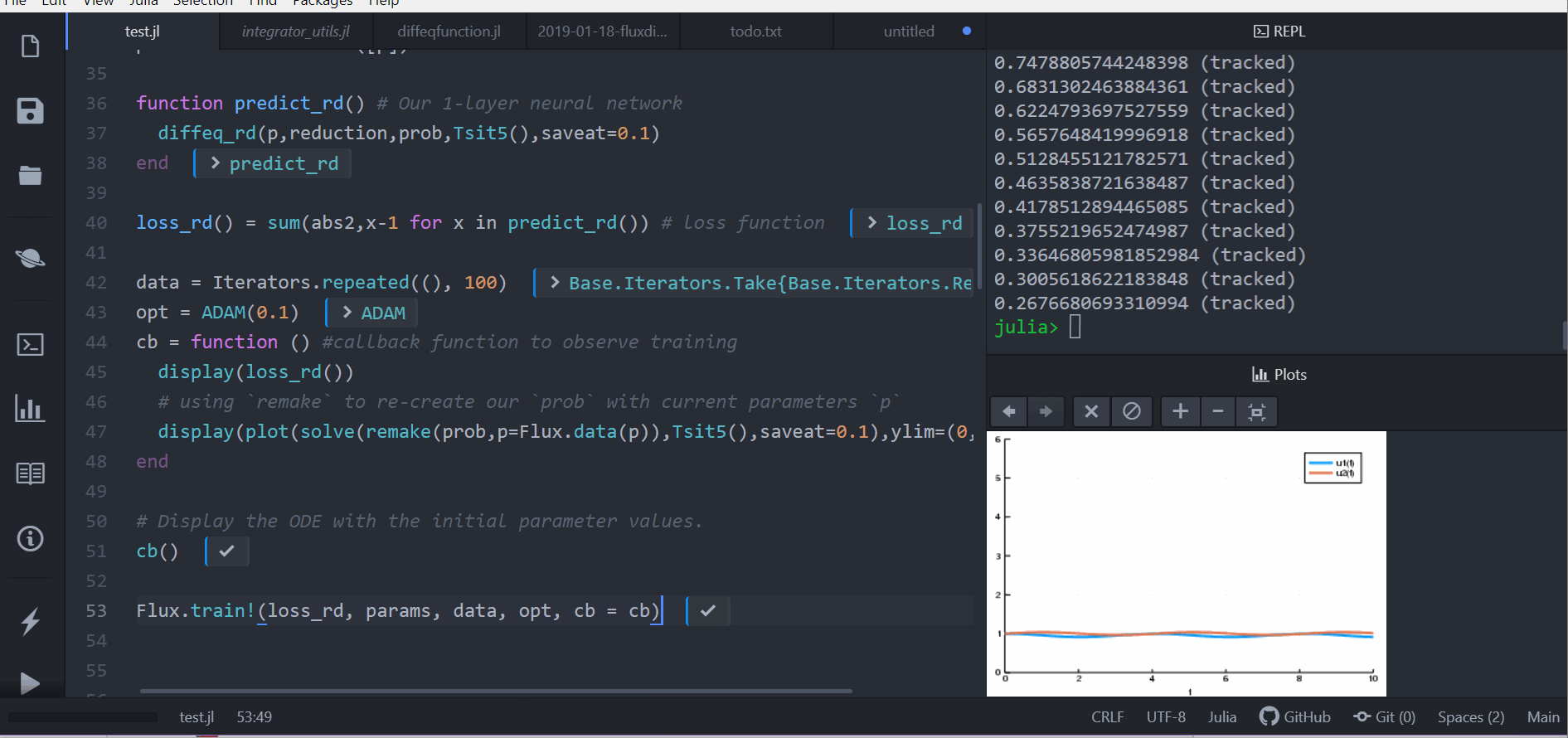
The results of the MATLAB simulation for the car suspension system.
Vectorization is applied in a few places, for example, in the standard library vector method call, but produces 4.16% slowdown.įigure 2.5. Consequently, not much space is left for further optimizations and improvements.Īutoparallelization is done nowhere. In some cases, they aided parallelization by using synchronization through mutexes. Parallel segments were specified manually by experts, who knew their potential for parallelization (by profiling their execution times and inspecting data dependences).

Within this CPU2006 benchmark, parallelization is specified for some code segments by using the Adaptive Communication Environment, a cross-platform communication library. This benchmark extensively uses modern C++ features and libraries, such as Boost. It uses the homonymous C++ library, which provides support for adaptivity through the appropriate complex data structures and algorithms. This benchmark is a partial differential equation solver based on the adaptive finite element method. Milutinović, in Advances in Computers, 2014 5.2.2 Dealii Now you can play around to find the solution of the text book.Aleksandar Vitorović. Let's first see if we can indeed meet your book's approximation, which does hold x is in a steady state it's derivative is zero. So the problem you're running into is that Mathematica's just not able to solve the differential equations exactly given the constraints you've offered.
#Differential system of equations solver update#
Update Added going beyond the text perturbatively with comparison against numerics.


 0 kommentar(er)
0 kommentar(er)
